Χαρακτηριστικά Heptagonal Prism και πώς να υπολογίσετε τον τόμο

Α επταγωνικό πρίσμα είναι μια γεωμετρική μορφή που, όπως υποδηλώνει το όνομα, περιλαμβάνει δύο γεωμετρικούς ορισμούς που είναι: πρίσμα και heptagon.

Ένα "πρίσμα" είναι μια γεωμετρική μορφή που περιορίζεται από δύο βάσεις που είναι ίσα και παράλληλα πολύγωνα και οι πλευρικές τους όψεις είναι παράλληλα γραφήματα.

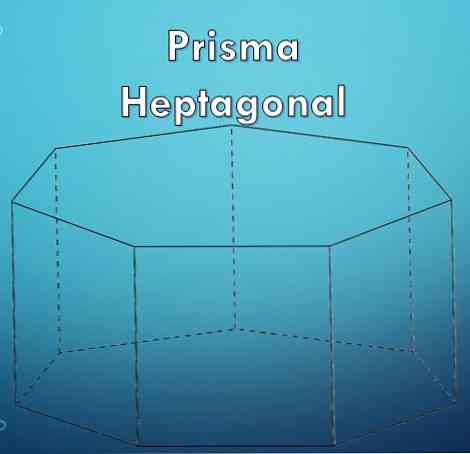
Ένα "heptagon" είναι ένα πολύγωνο που σχηματίζεται από επτά (7) πλευρές. Δεδομένου ότι ένα heptagon είναι ένα πολύγωνο, ίσως είναι κανονικό ή ακανόνιστο.

Ένα πολύγωνο λέγεται ότι είναι κανονικό αν όλες οι πλευρές του έχουν το ίδιο μήκος και οι εσωτερικές γωνίες τους μετρούν το ίδιο, ονομάζονται επίσης ισόπλευρα πολύγωνα. διαφορετικά λέγεται ότι το πολύγωνο είναι ακανόνιστο.

Χαρακτηριστικά ενός Heptagonal Prism

Ακολουθούν ορισμένα χαρακτηριστικά που έχουν ένα επταγωνικό πρίσμα όπως: η κατασκευή του, οι ιδιότητες των βάσεων του, η περιοχή όλων των προσώπων και ο όγκος του.

1- Κατασκευή

Για να κατασκευαστεί ένα επταγωνικό πρίσμα χρειάζονται δύο heptagons, που θα είναι οι βάσεις του και επτά parallelograms, ένα σε κάθε πλευρά του heptagon.

Ξεκινήστε σχεδιάζοντας ένα heptagon και στη συνέχεια τραβείτε επτά κάθετες γραμμές ίσου μήκους που προέρχονται από κάθε μία από τις κορυφές του.

Τελικά ένας άλλος heptagon τραβιέται έτσι ώστε οι κορυφές του να συμπίπτουν με το άκρο των γραμμών που έχουν τραβηχτεί στο προηγούμενο βήμα.

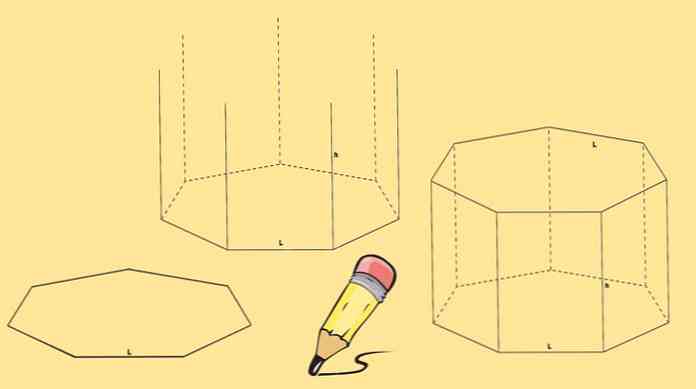
Το επταγωνικό πρίσμα που αναφέρθηκε παραπάνω ονομάζεται ευθεία επταγωνικό πρίσμα. Αλλά μπορείτε επίσης να έχετε ένα λοξό επταγωνικό πρίσμα όπως αυτό στο παρακάτω σχήμα.

2- Ιδιότητες των βάσεων

Δεδομένου ότι οι βάσεις τους είναι επτάνιοι, συμμορφώνονται ότι ο διαγώνιος αριθμός είναι D = nx (n-3) / 2, όπου "n" είναι ο αριθμός πλευρών του πολυγώνου. στην περίπτωση αυτή έχουμε D = 7 × 4/2 = 14.

Μπορούμε επίσης να δούμε ότι το άθροισμα των εσωτερικών γωνιών οποιουδήποτε heptagon (κανονικό ή ακανόνιστο) είναι ίσο με 900º. Αυτό μπορεί να επιβεβαιωθεί από την παρακάτω εικόνα.

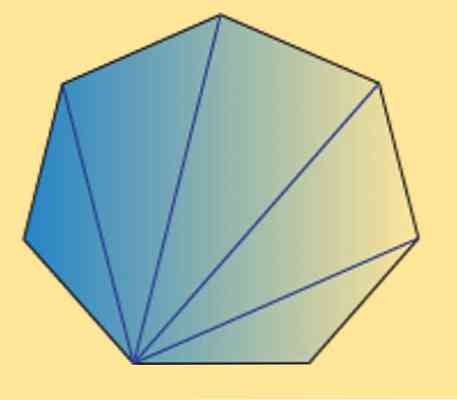
Όπως μπορεί να φανεί, υπάρχουν πέντε εσωτερικά τρίγωνα, και χρησιμοποιώντας το άθροισμα των εσωτερικών γωνιών ενός τριγώνου είναι ίσο με 180, μπορείτε να αποκτήσετε το επιθυμητό αποτέλεσμα.

3- Περιοχή που απαιτείται για την κατασκευή ενός Heptagonal Prism

Όπως βάσεις είναι heptagons και δύο πλευρές είναι παραλληλόγραμμα επτά, το εμβαδόν που απαιτείται για την κατασκευή ενός εξαγωνικό πρίσμα είναι ίση με + 2χΗ 7xp όπου «H» είναι η περιοχή του κάθε επτάγωνο και «Ρ» η περιοχή του κάθε παραλληλογράμμου.

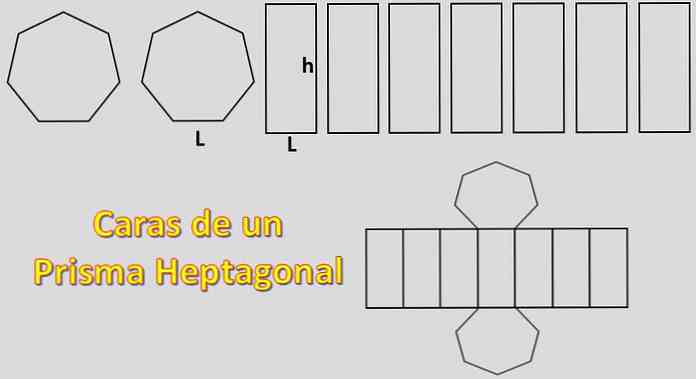
Σε αυτή την περίπτωση, υπολογίζεται η περιοχή ενός τακτικού heptagon. Γι 'αυτό είναι σημαντικό να γνωρίζουμε τον ορισμό του αποθέματος.

Το απόθεμα είναι μια κάθετη γραμμή που πηγαίνει από το κέντρο ενός κανονικού πολύγωνου στο μέσο της οποιασδήποτε πλευράς.

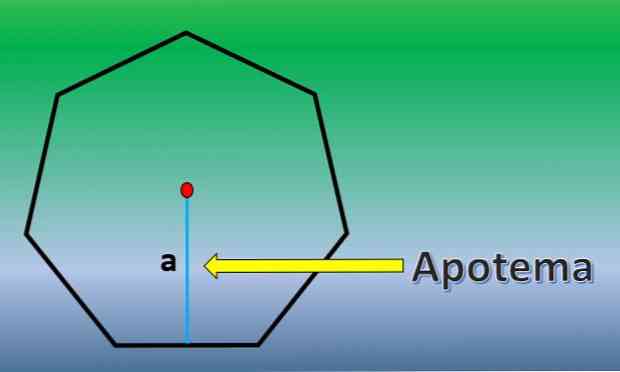
Μόλις γνωστή περιοχή apotema έχει να επτάγωνο είναι Η = 7xLxa / 2, όπου «L» είναι το μήκος της κάθε πλευράς και «a» μήκος apotema.

Η περιοχή ενός παραλληλογράμμου είναι εύκολο να υπολογιστεί, ορίζεται ως Ρ = Lxh, όπου «L» είναι το ίδιο μήκος πλευράς επτάγωνο και «h» είναι το ύψος του πρίσματος.

Εν κατακλείδι, το ποσό που απαιτείται για την κατασκευή ενός επτάγωνος υλικό πρίσματος (τακτική βάση) είναι 7xLxa + 7xLxh, δηλαδή 7XL (α + Η).

4- Ένταση ήχου

Μόλις είναι γνωστή η περιοχή μιας βάσης και το ύψος του πρίσματος, ο όγκος ορίζεται ως (βασική περιοχή) x (ύψος).

Στην περίπτωση ενός επταγωνικού πρίσματος (με κανονική βάση) έχει ότι ο όγκος του είναι V = 7xLxaxh / 2. μπορεί επίσης να γραφτεί ως V = Pxaxh / 2, όπου "P" είναι η περίμετρος του κανονικού heptagon.

Αναφορές

1. Billstein, R., Libeskind, S., & Lott, J.W. (2013). Μαθηματικά: μια προσέγγιση επίλυσης προβλημάτων για τους δασκάλους της βασικής εκπαίδευσης. López Mateos Editores.
2. Fregoso, R.S., & Carrera, S.A. (2005). Μαθηματικά 3. Συντάκτης Progreso.
3. Gallardo, G., & Pilar, Ρ. Μ. (2005). Μαθηματικά 6. Συντάκτης Progreso.
4. Gutiérrez, C. Τ., & Cisneros, Μ. Ρ. (2005). 3ο μάθημα μαθηματικών. Συντάκτης Progreso.
5. Kinsey, L., & Moore, Τ. Ε. (2006). Συμμετρία, Σχήμα και Διάστημα: Εισαγωγή στα Μαθηματικά Μέσω Γεωμετρίας (εικονογραφημένο, εκτύπωση εκ νέου). Springer Science & Business Media.
6. Mitchell, C. (1999). Εκπληκτικά σχέδια γραμμών μαθημάτων (Illustrated ed.). Scholastic Inc..
7. R., Μ. Ρ. (2005). Τραβήξω 6ο. Συντάκτης Progreso.