Πόσα άξονες συμμετρίας έχει ένας κύκλος;
Το άξονες συμμετρίας ενός κύκλου Είναι άπειρες. Αυτοί οι άξονες είναι εκείνοι που διαιρούν κάθε γεωμετρικό σχήμα σε δύο ακριβώς ίσα μισά.
Και ένας κύκλος αποτελείται από όλα τα σημεία των οποίων η απόσταση σε ένα σταθερό σημείο είναι μικρότερη ή ίση με μια ορισμένη τιμή "r".
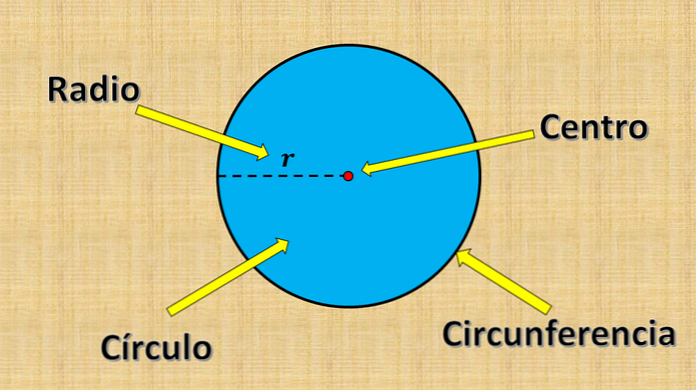
Το σταθερό σημείο που αναφέρεται παραπάνω ονομάζεται κέντρο και η τιμή "r" ονομάζεται ακτίνα. Η ακτίνα είναι η μεγαλύτερη απόσταση που μπορεί να υπάρχει μεταξύ ενός σημείου στον κύκλο και στο κέντρο.
Από την άλλη πλευρά, κάθε τμήμα γραμμής των οποίων τα άκρα είναι στην άκρη του κύκλου (περιφέρεια) και διέρχεται από το κέντρο ονομάζεται διάμετρος. Η μέτρησή του είναι πάντα ίση με το διπλάσιο της ακτίνας.
Κύκλος και περιφέρεια
Μη συγχέετε έναν κύκλο με έναν κύκλο. Η περιφέρεια αναφέρεται μόνο στα σημεία που βρίσκονται σε απόσταση "r" από το κέντρο. δηλαδή, μόνο την άκρη του κύκλου.
Ωστόσο, όταν ψάχνετε για τους άξονες συμμετρίας, είναι αδιάφορο αν εργάζεστε με κύκλο ή με κύκλο.
Τι είναι ένας άξονας συμμετρίας?
Ένας άξονας συμμετρίας είναι μια γραμμή που χωρίζει σε δύο ίσα μέρη ένα συγκεκριμένο γεωμετρικό σχήμα. Με άλλα λόγια, ένας άξονας συμμετρίας ενεργεί σαν καθρέφτης.
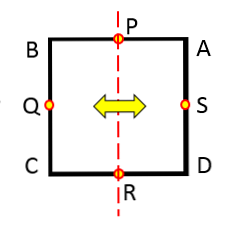
Άξονες συμμετρίας ενός κύκλου
Εάν παρατηρήσετε οποιοδήποτε κύκλο, ανεξάρτητα από την ακτίνα του, μπορείτε να δείτε ότι δεν είναι κάθε γραμμή που το διασχίζει είναι άξονας συμμετρίας.
Για παράδειγμα, καμία από τις γραμμές που αναγράφονται στην παρακάτω εικόνα δεν είναι άξονας συμμετρίας.
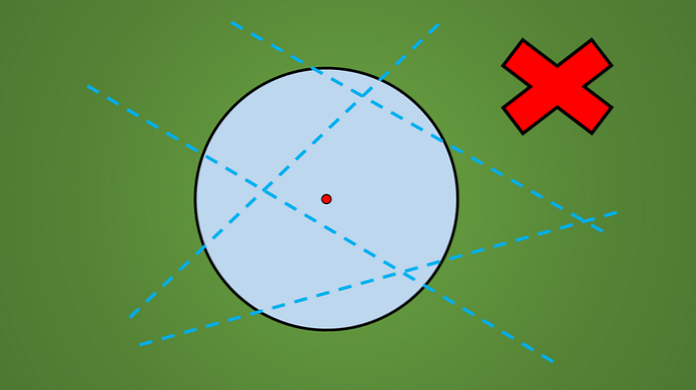
Ένας εύκολος τρόπος να ελέγξετε αν μια γραμμή είναι ένας άξονας συμμετρίας ή όχι είναι να αντικατοπτρίσετε κάθετα το γεωμετρικό σχήμα στην αντίθετη πλευρά της γραμμής.
Εάν η αντανάκλαση δεν ταιριάζει με το αρχικό σχήμα, τότε αυτή η γραμμή δεν είναι άξονας συμμετρίας. Η παρακάτω εικόνα απεικονίζει αυτή την τεχνική.
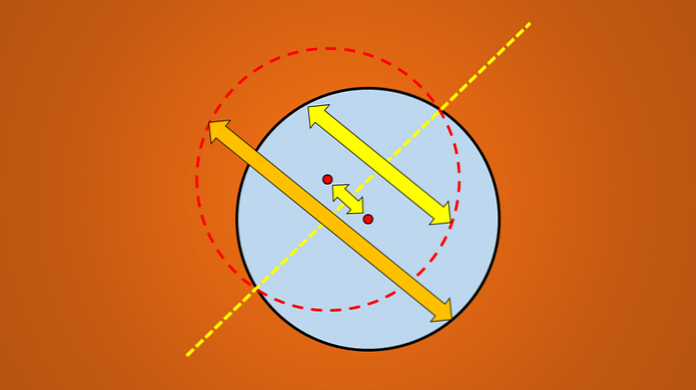
Αλλά εάν ληφθεί υπόψη η εικόνα που ακολουθεί, είναι γνωστό ότι η γραμμή που τραβιέται είναι ένας άξονας συμμετρίας του κύκλου.
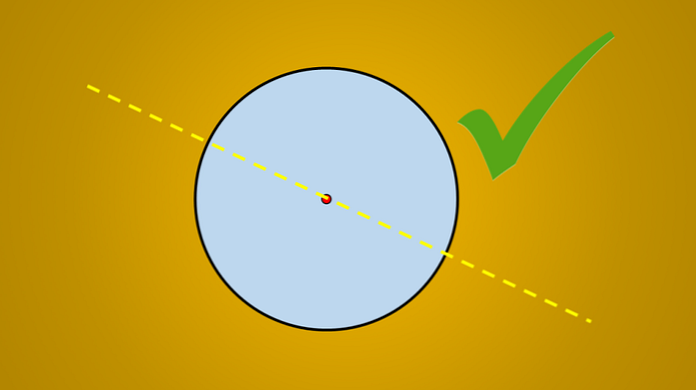
Το ερώτημα είναι: υπάρχουν περισσότεροι άξονες συμμετρίας; Η απάντηση είναι ναι. Εάν περιστρέψετε αυτή τη γραμμή κατά 45 ° αριστερόστροφα, η γραμμή που λαμβάνεται είναι επίσης ένας άξονας συμμετρίας του κύκλου.
Το ίδιο συμβαίνει και αν περιστρέψετε 90 °, 30 °, 8 ° και, γενικά, οποιοδήποτε αριθμό μοίρες.
Το σημαντικό για αυτές τις γραμμές δεν είναι η κλίση που έχουν, αλλά όλοι περνούν από το κέντρο του κύκλου. Επομένως, οποιαδήποτε γραμμή που περιέχει μια διάμετρο του κύκλου είναι ένας άξονας συμμετρίας.
Έτσι, αφού ένας κύκλος έχει άπειρο αριθμό διαμέτρων, τότε έχει έναν άπειρο αριθμό αξόνων συμμετρίας.
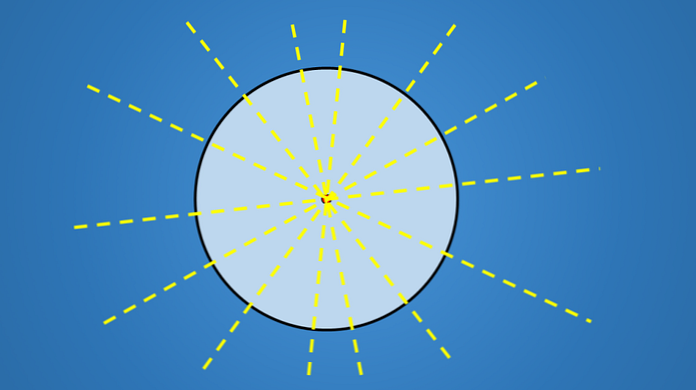
Άλλες γεωμετρικές μορφές, όπως ένα τρίγωνο, ένα τετράπλευρο, ένα πεντάγωνο, ένα εξάγωνο ή οποιοδήποτε άλλο πολύγωνο, έχουν έναν πεπερασμένο αριθμό αξόνων συμμετρίας.
Ο λόγος για τον οποίο ένας κύκλος έχει έναν άπειρο αριθμό αξόνων συμμετρίας είναι ότι δεν έχει πλευρές.
Αναφορές
- Basto, J. R. (2014). Μαθηματικά 3: Βασική αναλυτική γεωμετρία. Συντακτική ομάδα Patria.
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Μαθηματικά: μια προσέγγιση επίλυσης προβλημάτων για τους δασκάλους της βασικής εκπαίδευσης. López Mateos Editores.
- Bult, Β., & Hobbs, D. (2001). Μαθηματικό λεξικό (εικονογραφημένη έκδοση). (F. P. Cadena, Trad.) Εκδόσεις AKAL.
- Callejo, Ι., Aguilera, Μ., Martinez, L. & Aldea, C. (1986). Μαθηματικά Γεωμετρία Μεταρρύθμιση του ανώτερου κύκλου του E.G.B. Υπουργείο Παιδείας.
- Schneider, W. & Sappert, D. (1990). Πρακτικό εγχειρίδιο τεχνικής κατάρτισης: εισαγωγή στα βασικά τεχνικά σχέδια. Επαναστροφή.
- Thomas, G. Β., & Weir, Μ. D. (2006). Υπολογισμός: πολλές μεταβλητές. Εκπαίδευση Pearson.


