Αρχιμήδης Βιογραφία, συμβολές και εφευρέσεις

Αρχιμήδης των Συρακουσών (287 π.Χ. - 212 π.Χ) ήταν μαθηματικός, φυσικός, εφευρέτης, μηχανικός και Έλληνας αστρονόμος από την αρχαία πόλη των Συρακουσών στο νησί της Σικελίας. Οι σημαντικότερες συνεισφορές του είναι η αρχή του Αρχιμήδη, η ανάπτυξη της μεθόδου εκταμίευσης, η μηχανική μέθοδος ή η δημιουργία του πρώτου πλανητάριου.

Αυτή τη στιγμή θεωρείται ως ένα από τα τρία πιο σημαντικά στοιχεία στα μαθηματικά της αρχαιότητας με Ευκλείδης και ο Απολλώνιος, ως συνεισφορά τους σήμαινε σημαντικές επιστημονικές πρόοδοι προς το παρόν στους τομείς της λογισμός, φυσική, τη γεωμετρία και την αστρονομία. Με τη σειρά του, αυτό τον καθιστά έναν από τους κορυφαίους επιστήμονες στην ιστορία της ανθρωπότητας. 

Αν και μερικές λεπτομέρειες της προσωπικής του ζωής και εκείνες που είναι γνωστές είναι αμφίβολη η αξιοπιστία γνωστό, οι εισφορές τους που είναι γνωστό χάρη σε μια σειρά γραπτών επιστολών για το έργο και τα επιτεύγματα τους, που έχουν διατηρηθεί μέχρι σήμερα, που ανήκουν στην αλληλογραφία που κράτησε για χρόνια με φίλους και άλλους μαθηματικούς της εποχής.

Ο Αρχιμήδης ήταν διάσημος στην εποχή του χάρη στις εφευρέσεις του, οι οποίες προσελκύουν την προσοχή των συγχρόνων του, εν μέρει επειδή χρησιμοποιούνταν ως συσκευές πολέμου για να αποφύγουν επιτυχώς πολλές ρωμαϊκές εισβολές..

Ωστόσο, λέγεται ότι ισχυρίστηκε ότι το μόνο σημαντικό πράγμα ήταν τα μαθηματικά και ότι οι εφευρέσεις του ήταν απλώς ένα προϊόν του χόμπι της εφαρμοσμένης γεωμετρίας. Στην επόμενη γενιά, τα έργα του σε καθαρά μαθηματικά έχουν εκτιμηθεί πολύ περισσότερο από τις εφευρέσεις του.

Ευρετήριο

• 1 Βιογραφία
  • 1.1 Εκπαίδευση
  • 1.2 Επιστημονική εργασία
  • 1.3 Σύγκρουση στις Συρακούσες
  • 1.4 Θάνατος
• 2 Επιστημονικές συνεισφορές του Αρχιμήδη
  • 2.1 Η αρχή του Αρχιμήδη
  • 2.2 Μηχανική μέθοδος
  • 2.3 Επεξήγηση του νόμου του μοχλού
  • 2.4 Ανάπτυξη της μεθόδου εξόρυξης ή εξάντλησης για την επιστημονική επίδειξη
  • 2.5 Το μέτρο του κύκλου
  • 2.6 Η γεωμετρία των σφαιρών και των κυλίνδρων
• 3 Εφευρέσεις
  • 3.1 Το χιλιομετρητή
  • 3.2 Το πρώτο πλανητάριο
  • 3.3 Η βίδα του Αρχιμήδη
  • 3.4 Το νύχι του Αρχιμήδη
• 4 Αναφορές

Βιογραφία

Ο Αρχιμήδης των Συρακουσών γεννήθηκε περίπου το έτος 287 π.Χ. Δεν γνωρίζουν πολλά στοιχεία για τα πρώτα του χρόνια, αν και μπορεί να λεχθεί ότι γεννήθηκε στη Συρακούζη, μια πόλη που θεωρείται το κύριο λιμάνι της Σικελίας, σήμερα στην Ιταλία..

Εκείνη την εποχή, Συρακούσες ήταν μία από τις πόλεις που αποτελούσαν την λεγόμενη Magna Grecia, η οποία κατοικήθηκε χώρο αποίκους ελληνικής καταγωγής στη νότια περιοχή της ιταλικής χερσονήσου και της Σικελίας.

Δεν υπάρχουν γνωστά γεγονότα για τη μητέρα του Αρχιμήδη. Σε σχέση με τον πατέρα, είναι γνωστό ότι αυτό ονομάστηκε Φειδίας και ότι ήταν αφοσιωμένος στην αστρονομία. Αυτές οι πληροφορίες του πατέρα του είναι γνωστές χάρη σε ένα κομμάτι του βιβλίου Ο μετρητής άμμου, που γράφτηκε από τον Αρχιμήδη, όπου αναφέρει το όνομα του πατέρα του.

Ο Ηράκλειδης, ο οποίος ήταν Έλληνας φιλόσοφος και αστρονόμος, αγαπούσε τον Αρχιμήδη και μάλιστα έγραψε μια βιογραφία γι 'αυτόν. Ωστόσο, το έγγραφο αυτό δεν έχει διατηρηθεί, επομένως όλες οι πληροφορίες που περιέχονται σε αυτό δεν είναι γνωστές.

Επιπλέον, ο ιστορικός, φιλόσοφος και βιογράφος Πλούταρχος αναφέρει στο βιβλίο Παράλληλη του ζει ότι ο Αρχιμήδης είχε σχέση με το αίμα να Hiero II, έναν τύραννο ο οποίος διέταξε στις Συρακούσες από το 265 π.Χ..

Εκπαίδευση

Ως αποτέλεσμα των ελάχιστων πληροφοριών που έχουμε σχετικά με τον Αρχιμήδη, δεν γνωρίζουμε με βεβαιότητα πού πήρε την πρώτη εκπαίδευσή του.

Ωστόσο, διάφοροι ιστοριογράφοι έχουν διαπιστώσει ότι υπάρχει μεγάλη πιθανότητα ο Αρχιμήδης να σπουδάσει στην Αλεξάνδρεια, το σημαντικότερο ελληνικό πολιτιστικό και διδακτικό κέντρο στην περιοχή..

Η υπόθεση αυτή υποστηρίζεται από τις πληροφορίες που προσφέρει ο Έλληνας ιστορικός Diodoro Sículo, ο οποίος ανέφερε ότι ο Αρχιμήδης πιθανώς σπούδασε στην Αλεξάνδρεια.

Επιπλέον, σε πολλά από τα έργα του, ο ίδιος ο Αρχιμήδης αναφέρει άλλους επιστήμονες της εποχής, των οποίων η εργασία συγκεντρώθηκε στην Αλεξάνδρεια, ώστε να μπορεί να υποτεθεί ότι στην πραγματικότητα αναπτύχθηκε σε αυτή την πόλη.

Μερικές προσωπικότητες οι οποίες πιστεύεται ότι Αρχιμήδη αλληλεπιδράσει στην Αλεξάνδρεια γεωγράφος, μαθηματικός και αστρονόμος Erathostenes Κυρήνη, και μαθηματικών και αστρονόμος Κόνων Sanos.

Οικογενειακό κίνητρο

Από την άλλη πλευρά, το γεγονός ότι ο πατέρας του Αρχιμήδη ήταν ο αστρονόμος μπορεί να έχουν επηρεάσει σημαντικά τις κλίσεις αργότερα demostróe γιατί αργότερα και από νεαρή ηλικία, ήταν εμφανής στο πρόσωπό του μια ιδιαίτερη έλξη στην περιοχή της επιστήμες.

Μετά τον καιρό του στην Αλεξάνδρεια, εκτιμάται ότι ο Αρχιμήδης επέστρεψε στις Συρακούσες.

Επιστημονική εργασία

Μετά την επιστροφή του στη Συρακούσα, ο Αρχιμήδης άρχισε να σχεδιάζει διαφορετικά αντικείμενα που σύντομα του κέρδισαν μια ορισμένη δημοτικότητα μεταξύ των κατοίκων αυτής της πόλης. Σε αυτή την περίοδο έδωσε τον εαυτό του εντελώς στο επιστημονικό έργο, παρήγαγε διαφορετικές εφευρέσεις και συνήγαγε αρκετές μαθηματικές έννοιες πολύ προχωρημένες στην εποχή του.

Για παράδειγμα, όταν αφιερώθηκε στη μελέτη των χαρακτηριστικών των συμπαγών καμπύλων και επίπεδων μορφών, κατέληξε σε έννοιες σχετικές με τον ενσωματωμένο και τον διαφορικό λογισμό, ο οποίος αναπτύχθηκε αργότερα.

Επίσης, Αρχιμήδη ο οποίος ορίζεται ο όγκος που συνδέεται με μια περιοχή που αντιστοιχεί στο διπλάσιο του μεγέθους του κυλίνδρου που περιέχει, και ήταν που εφηύρε την ένωση τροχαλία, με βάση τα ευρήματά τους σχετικά με το δίκαιο του μοχλού.

Σύγκρουση στις Συρακούσες

Κατά τη διάρκεια του έτους 213 π.Χ., οι Ρωμαίοι στρατιώτες εισήλθαν στην πόλη των Συρακουσών και περιχώρησαν τους εποίκους τους για να τους οδηγήσουν στην παράδοση.

Η δράση αυτή έγινε υπό την καθοδήγηση του στρατιωτικού και του ελληνικού πολιτικού Marco Claudio Marcelo στο πλαίσιο του δεύτερου πολυνικού πολέμου. Αργότερα, ήταν γνωστό ως το ξίφος της Ρώμης, αφού κατέληξε στην κατάκτηση των Συρακουσών.

Στη μέση της σύγκρουσης, η οποία διήρκεσε δύο χρόνια, οι κάτοικοι των Συρακουσών από τους Ρωμαίους πολέμησε με θάρρος και αγριότητα, και ο Αρχιμήδης έπαιξε πολύ σημαντικό ρόλο, δεδομένου ότι ασχολείται με τη δημιουργία εργαλείων και μέσων που βοηθούν νίκησε τους Ρωμαίους.

Τέλος, ο Marco Claudio Marcelo πήρε την πόλη των Συρακουσών. Πριν από τη μεγάλη πνευματικότητα του Αρχιμήδη, ο Μαρσέλο διέταξε να μην τραυματιστούν ή να σκοτωθούν. Ωστόσο, ο Αρχιμήδης σκοτώθηκε στα χέρια ενός Ρωμαίου στρατιώτη.

Θάνατος

Ο Αρχιμήδης πέθανε το έτος 212 π.Χ. Περισσότερα από 130 χρόνια μετά το θάνατό του, το έτος 137 π.Χ., συγγραφέας, πολιτικός και φιλόσοφος Marcus Tullius Cicero κατέλαβαν μια θέση στη διοίκηση της Ρώμης και ήθελε να βρει τον τάφο του Αρχιμήδη.

Αυτό το καθήκον δεν ήταν εύκολο, αφού ο Cicero δεν βρήκε κανέναν να δείξει τον ακριβή τόπο. Εντούτοις, τελικά το πήρε, πολύ κοντά στην πόρτα του Agrigento και σε αξιοθρήνητες συνθήκες.

Ο Κικέρωνα καθαρίζει τον τάφο και ανακαλύπτει ότι ήταν εγγεγραμμένος με μια σφαίρα μέσα σε έναν κύλινδρο, ως αναφορά στην ανακάλυψη για τον τόμο που έκανε ο Αρχιμήδης πριν από λίγο καιρό..

Εκδόσεις για το θάνατό του

Πρώτη έκδοση

Μία από τις εκδοχές αναφέρει ότι ο Αρχιμήδης βρισκόταν στη μέση της επίλυσης ενός μαθηματικού προβλήματος όταν προσεγγίσθηκε από έναν Ρωμαίο στρατιώτη. Λέγεται ότι ο Αρχιμήδης θα μπορούσε να του ζήτησε κάποιο χρόνο για να λύσει το πρόβλημα, οπότε ο στρατιώτης θα τον σκότωσε.

Δεύτερη έκδοση

Η δεύτερη έκδοση είναι παρόμοια με την πρώτη. Λογαριασμός που ο Αρχιμήδης επιλύει ένα πρόβλημα μαθηματικών όταν έλαβε χώρα η λήψη της πόλης.

Ένας ρωμαϊκός στρατιώτης μπήκε στην ένωσή του και του διέταξε να συναντήσει τον Μαρσέλο και ο Αρχιμήδης απάντησε ότι έπρεπε να λύσει το πρόβλημα στο οποίο εργαζόταν πρώτα. Ο στρατιώτης αναστάτωσε ως αποτέλεσμα αυτής της απάντησης και τον σκότωσε.

Τρίτη έκδοση

Αυτή η υπόθεση δείχνει ότι ο Αρχιμήδης είχε στα χέρια του μια μεγάλη ποικιλία μέσων που είναι τυπικά των μαθηματικών. Στη συνέχεια, ένας στρατιώτης τον είδε και σκέφτηκε ότι μπορεί να φέρει πολύτιμα αντικείμενα, οπότε τον σκότωσε.

Τέταρτη έκδοση

Αυτή η εκδοχή δείχνει ότι ο Αρχιμήδης συγκρατήθηκε κοντά στο έδαφος, σχεδιάζοντας σχέδια που μελετούσε. Προφανώς, ένας Ρωμαίος στρατιώτης ήρθε από πίσω και, χωρίς να γνωρίζει ότι ήταν ο Αρχιμήδης, τον πυροβόλησε.

Επιστημονική συνεισφορά του Αρχιμήδη

Η αρχή του Αρχιμήδη

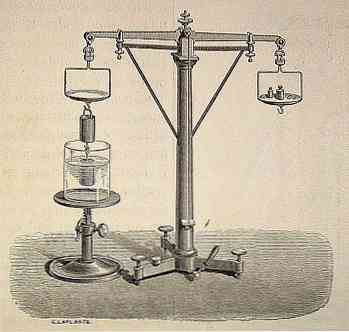
Η αρχή του Αρχιμήδη θεωρείται από τη σύγχρονη επιστήμη ως μία από τις σημαντικότερες κληρονομιές της αρχαίας εποχής.

Σε όλη την ιστορία, και από του στόματος maneral, έχει παραδοθεί Αρχιμήδης ήρθε στην ανακάλυψη του κατά λάθος χάρη στο βασιλιά Hiero θα αναθέσει ελέγξει κατά πόσον ένα χρυσό στεφάνι ανέθεσε να κάνει γι 'αυτόν ήταν μόνο ο χρυσός καθαρό και δεν περιέχει κανένα άλλο μέταλλο. Έπρεπε να το φέρω χωρίς να καταστρέψω το στέμμα.

Λέγεται ότι ενώ ο Αρχιμήδης διαλογιζόταν πώς να λύσει αυτό το πρόβλημα αποφάσισε να κάνει μπάνιο και όταν εισήλθε στην μπανιέρα συνειδητοποίησε ότι το νερό αυξήθηκε σε επίπεδο όταν βυθίστηκε μέσα του..

Έτσι, έρχονται να ανακαλύψουν την επιστημονική αρχή ότι «κάθε οργανισμός ολικώς ή μερικώς βυθισμένες σε ένα ρευστό (υγρό ή αέριο) δέχεται μια προς τα πάνω, είναι ίσο με το βάρος της ώσης ρευστού μετατοπίζεται από το αντικείμενο».

Η αρχή αυτή σημαίνει ότι τα υγρά ασκούν μία ανοδική δύναμη η οποία ωθεί προς τα άνω-οποιοδήποτε αντικείμενο βυθίζεται σε αυτά, και ότι το ποσό του παρόντος άνωση ισούται με το βάρος του υγρού που μετατοπίζεται από το βυθισμένο σώμα, ανεξάρτητα από το βάρος.

Η εξήγηση αυτής της αρχής περιγράφει το φαινόμενο της επίπλευσης και βρίσκεται στο δικό της Συνθήκη επί πλωτών σωμάτων.

Η αρχή του Αρχιμήδη έχει εφαρμοστεί σε μεγάλες ποσότητες για την πλεύση αντικειμένων μαζικής χρήσης όπως υποβρύχια, πλοία, ναυαγοσώστες και μπαλόνια.

Μηχανική μέθοδος

Μια άλλη από τις πιο σημαντικές συνεισφορές στην επιστήμη Αρχιμήδη ήταν η συμπερίληψη ενός αμιγώς μηχανική μέθοδος -που λένε, τεχνική λογική και επιχειρηματολογία των γεωμετρικών προβλημάτων, που σήμαινε μια πρωτοφανή τρόπο για να λύσει αυτά τα προβλήματα για την ώρα.

Στο πλαίσιο του Αρχιμήδη, η γεωμετρία θεωρήθηκε ως μια αποκλειστικά θεωρητική επιστήμη και το κοινό ήταν ότι τα καθαρά μαθηματικά καταγόταν προς άλλες πρακτικές επιστήμες στις οποίες θα μπορούσαν να εφαρμοστούν οι αρχές της..

Για το λόγο αυτό, θεωρείται σήμερα ως πρόδρομος της μηχανικής ως επιστημονικής πειθαρχίας.

Στην επιστολή με την οποία η μαθηματική εκθέτει τη νέα μέθοδο στο φίλο του Ερατοσθένη, αυτό δείχνει ότι μπορεί να αντιμετωπίσει τα θέματα των μαθηματικών μέσα από τους μηχανικούς, και κατά κάποιο τρόπο είναι πιο εύκολο να οικοδομήσουμε την επίδειξη ενός γεωμετρικού θεωρήματος, αν έχει ήδη έχει κάποια προηγούμενη πρακτική γνώση ότι αν δεν έχετε την παραμικρή ιδέα γι 'αυτό.

Αυτή η νέα μέθοδος διερεύνησης που διεξήγαγε ο Αρχιμήδης θα γίνει ο πρόδρομος του άτυπου σταδίου της ανακάλυψης και της διατύπωσης υποθέσεων της σύγχρονης επιστημονικής μεθόδου.

Επεξήγηση του νόμου του μοχλού

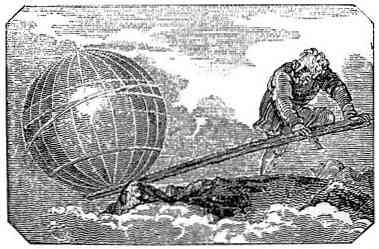
Ενώ ο μοχλός είναι ένα απλό μηχάνημα που χρησιμοποιήθηκε πολύ νωρίτερα από τον Αρχιμήδη, ήταν αυτός που διατύπωσε την αρχή που εξηγεί τη λειτουργία του στην πραγματεία του για την ισορροπία των αεροσκαφών.

Στη διατύπωση αυτού του νόμου, ο Αρχιμήδης θεσπίζει αρχές που περιγράφουν τη διαφορετική συμπεριφορά ενός μοχλού κατά την τοποθέτηση δύο σωμάτων πάνω του, ανάλογα με το βάρος του και την απόστασή του από το σημείο στήριξης.

Με αυτό τον τρόπο, επισημαίνει ότι δύο όργανα που μπορούν να μετρηθούν (συναρμολογημένα), τοποθετημένα σε ένα μοχλό, είναι ισορροπημένα όταν βρίσκονται σε αποστάσεις αντιστρόφως ανάλογες με το βάρος τους.

Με τον ίδιο τρόπο, τα αμέτρητα σώματα (που δεν μπορούν να μετρηθούν) το κάνουν, αλλά ο νόμος αυτός ήταν αποδεκτός από τον Αρχιμήδη μόνο με σώματα πρώτου τύπου.

Διατύπωση της αρχής του μοχλού είναι ένα καλό παράδειγμα της εφαρμογής της μηχανικής μεθόδου, δεδομένου ότι, όπως εξηγήθηκε σε επιστολή προς Dositeo, ανακαλύφθηκε αρχικά μέσω μηχανικές μεθόδους που υλοποιούνται.

Αργότερα τα διαμόρφωσε χρησιμοποιώντας μεθόδους γεωμετρίας (θεωρητικές). Από αυτόν τον πειραματισμό στα σώματα, η έννοια του κέντρου βάρους αποκολλήθηκε.

Ανάπτυξη της μεθόδου εξόρυξης ή εξάντλησης για την επιστημονική επίδειξη

Η εξάντληση είναι μια μέθοδος που χρησιμοποιείται στη γεωμετρία, η οποία συνίσταται στην προσέγγιση των γεωμετρικών μορφών των οποίων η περιοχή είναι γνωστή, μέσω της επιγραφής και της περιγραφής, σε άλλη περιοχή της οποίας η περιοχή προορίζεται να είναι γνωστή..

Παρόλο που ο Αρχιμήδης δεν ήταν ο δημιουργός αυτής της μεθόδου, το ανέπτυξε αριστοτεχνικά, καταφέρνοντας να υπολογίσει μέσω αυτού μια ακριβή τιμή Pi.

Αρχιμήδη, χρησιμοποιώντας τη μέθοδο της εξάντλησης, και χαραγμένα εξάγωνα περιορίζονται σε μια περιφέρεια διαμέτρου 1 έως παράλογο μειώνοντας τη διαφορά μεταξύ της περιοχής των εξαγώνων και την περιφέρεια.

Για να γίνει αυτό, διέλυσε τα εξάγωνα δημιουργώντας πολύγωνα μέχρι 16 πλευρών, όπως φαίνεται στο προηγούμενο σχήμα.

Με αυτό τον τρόπο, ήρθε να διευκρινίσει ότι η τιμή του pi (της σχέσης μεταξύ του μήκους ενός κύκλου και της διαμέτρου του) είναι μεταξύ των τιμών 3.14084507 ... και 3.14285714 ... .

Αρχιμήδης χρησιμοποιείται αριστοτεχνικά τη μέθοδο της εξάντλησης, διότι όχι μόνο κατάφερε προσέγγιση για τον υπολογισμό της αξίας του π με ένα περιθώριο λάθους πολύ χαμηλή και ως εκ τούτου deseado-, αλλά και για να είναι μια παράλογη αριθμό Pi μέσω αυτή η μέθοδος και τα αποτελέσματα που ελήφθησαν έθεσε τα θεμέλια για να βλαστήσουν στο λογισμό του συστήματος, και στη συνέχεια, στη σύγχρονη ολοκληρωτικού λογισμού.

Το μέτρο του κύκλου

Για να προσδιορίσει την περιοχή ενός κύκλου, ο Archimedes χρησιμοποίησε μια μέθοδο που συνίστατο στο σχέδιο ενός τετραγώνου που ταιριάζει ακριβώς μέσα σε έναν κύκλο. 

Γνωρίζοντας ότι η περιοχή της πλατείας ήταν το άθροισμα των πλευρών της και ότι η περιοχή του κύκλου ήταν μεγαλύτερη, άρχισε να εργάζεται για την απόκτηση προσεγγίσεων. Αυτό το έπραξε αντικαθιστώντας το τετράγωνο με ένα πολύγωνο 6 όψεων και στη συνέχεια με πιο πολύπλοκα πολύγωνα.

Ο Αρχιμήδης ήταν ο πρώτος μαθηματικός της ιστορίας για να προσεγγίσει έναν σοβαρό υπολογισμό του αριθμού Pi.

Η γεωμετρία των σφαιρών και των κυλίνδρων

Μεταξύ των εννέα διατριβών που συνθέτουν το έργο του Αρχιμήδη στα μαθηματικά και τη φυσική, υπάρχουν δύο τόμοι σχετικά με τη γεωμετρία των σφαιρών και των κυλίνδρων.

Αυτή η εργασία ασχολείται με τον προσδιορισμό ότι η επιφάνεια οποιασδήποτε σφαίρας ακτίνας είναι τέσσερις φορές μεγαλύτερη από εκείνη του μεγαλύτερου κύκλου της και ότι ο όγκος μιας σφαίρας είναι τα δύο τρίτα εκείνης του κυλίνδρου στον οποίο είναι γραμμένο.

Εφευρέσεις

Το χιλιομετρητή

Επίσης γνωστό ως χιλιόμετρα, ήταν μια εφεύρεση αυτού του διάσημου ανθρώπου.

Αυτή η συσκευή κατασκευάστηκε με βάση την αρχή ενός τροχού που, όταν γυρίζει, ενεργοποιεί ταχύτητες που επιτρέπουν τον υπολογισμό της διανυθείσας απόστασης..

Σύμφωνα με αυτή την ίδια αρχή, ο Αρχιμήδης σχεδίασε διάφορους τύπους αποστάσεων για στρατιωτικούς και πολιτικούς σκοπούς.

Το πρώτο πλανητάριο

Με βάση τη μαρτυρία πολλών κλασικών συγγραφέων, όπως ο Κικέρων, ο Οβίδιος, Κλαυδίων, Marciano Καπέλα, Casiodoro, Σέξτος ο Εμπειρικός και Lactancio, σήμερα πολλοί επιστήμονες αποδίδουν στον Αρχιμήδη τη δημιουργία του πρώτου υποτυπώδη πλανητικό.

Είναι ένας μηχανισμός που αποτελείται από μια σειρά «σφαιρών» που κατάφεραν να μιμηθούν την κίνηση των πλανητών. Μέχρι στιγμής οι λεπτομέρειες αυτού του μηχανισμού είναι άγνωστες.

Σύμφωνα με τον Cicero, τα πλανητάρια που χτίστηκε από τον Αρχιμήδη ήταν δύο. Σε μία από αυτές εκπροσωπήθηκαν η γη και οι διάφοροι αστερισμοί κοντά.

Στην άλλη, με μια μόνο περιστροφή, ο ήλιος, το φεγγάρι και οι πλανήτες έκαναν τις δικές τους ανεξάρτητες κινήσεις σε σχέση με τα σταθερά αστέρια με τον ίδιο τρόπο που έκαναν σε μια πραγματική μέρα. Στο τελευταίο, επιπλέον, μπορούσαν να παρατηρηθούν διαδοχικές φάσεις και εκλείψεις της σελήνης.

Η βίδα του Αρχιμήδη

Ο κοχλίας Archimedes είναι μια συσκευή που χρησιμοποιείται για τη μεταφορά νερού από κάτω προς τα πάνω σε μια πλαγιά, χρησιμοποιώντας έναν σωλήνα ή έναν κύλινδρο.

Σύμφωνα με την ελληνική ιστορικός Διόδωρος, χάρη σε αυτή την εφεύρεση άρδευση της εύφορης γης που βρίσκεται κατά μήκος του Νείλου στην αρχαία Αίγυπτο είχε προβλεφθεί δεδομένου ότι τα παραδοσιακά εργαλεία που απαιτούνται για μια τεράστια σωματική προσπάθεια εξαντληθεί εργαζομένων.

Ο χρησιμοποιούμενος κύλινδρος έχει μέσα σε μια βίδα του ίδιου μήκους, η οποία διατηρεί διασυνδεδεμένο ένα σύστημα προπέλας ή πτερυγίων που εκτελούν μια περιστροφική κίνηση που κινείται χειροκίνητα από έναν περιστρεφόμενο μοχλό.

Με αυτόν τον τρόπο, οι έλικες καταφέρνουν να ωθήσουν οποιαδήποτε ουσία από κάτω προς τα πάνω, σχηματίζοντας ένα είδος άπειρου κυκλώματος.

Το νύχι του Αρχιμήδη

Το νύχι του Αρχιμήδη, ή το σιδερένιο χέρι όπως είναι επίσης γνωστή, ήταν ένα από τα πιο φοβερά όπλα του πολέμου που δημιουργούνται από αυτό το μαθηματικό, να γίνει η πιο σημαντική για την άμυνα της Σικελίας από τους ρωμαϊκούς επιδρομές.

Σύμφωνα με έρευνα που διεξήχθη από καθηγητές του Πανεπιστημίου του Drexel Chris Rorres (Τμήμα Μαθηματικών) και Harry Harris (Τμήμα Πολιτικών Μηχανικών και Αρχιτεκτόνων), ήταν ένα μεγάλο μοχλό που είχε ένα γάντζο αγωνίζεται συνδέεται με το μοχλό από μια αλυσίδα γύρω της.

Μέσα από το μοχλό έτσι ώστε το άγκιστρο έπεσε στο πλοίο εχθρός χειραγωγείται, και ο στόχος ήταν να το συνδέσετε και να αυξήσει την σε τέτοιο βαθμό ώστε η απελευθέρωση επιτεύχθηκε πλήρως ανατρέψει ή να κάνουν συντριβή ενάντια στους βράχους της ακτής.

Rorres και Harris που παρουσιάστηκε στο Συμπόσιο «Μηχανήματα και έκτακτες δομές της αρχαιότητας» (2001), ένα μικροσκοπικό εκπροσώπηση αυτής της συσκευής με τίτλο «Μια τρομερή πολεμική μηχανή: Κατασκευή και λειτουργία του σιδερένιο χέρι του Αρχιμήδη»

Για την πραγματοποίηση αυτού του έργου βασίστηκαν στα επιχειρήματα των αρχαίων ιστορικών Polibio, Plutarco και Tito Livio.

Αναφορές

1. ASSIS, Α. (2008). Τον Αρχιμήδη, το κέντρο βάρους και τον πρώτο νόμο της μηχανικής [online]. Πρόσβαση στις 10 Ιουνίου 2017 στο bourabai.ru.
2. DIJKSTERHUIS, Ε. (1956). Αρχιμήδης [online]. Πρόσβαση στις 9 Ιουνίου 2015 στο World Wide Web: books.google.co.ve/books.
3. MOLINA, Α. (2008). Η μέθοδος έρευνας του Αρχιμήδη των Συρακουσών: διαίσθηση, μηχανική και εξέγερση [online]. Πρόσβαση στις 10 Ιουνίου 2017 στο World Wide Webproduccioncientifica.luz.edu.
4. O'CONNOR, J. & ROBERTSON, R. (1999). Αρχιμήδης των Συρακουσών [online]. Πρόσβαση στις 9 Ιουνίου 2017 στο history.mcs.st-and.ac.uk.
5. PARRA, Ε. (2009). Archimedes: η ζωή του, τα έργα και οι συνεισφορές στα σύγχρονα μαθηματικά [online]. Ανακτήθηκε στις 9 Ιουνίου 2017 στο lfunes.uniandes.edu.co.
6. QUINN, L. (2005). Αρχιμήδης των Συρακουσών [online]. Πρόσβαση στις 9 Ιουνίου 2017 στο math.ucdenver.edu.
7. RORRES, C. & HARRIS, Η. (2001). Μια τρομερή πολεμική μηχανή: Κατασκευή και λειτουργία του σιδερένιου χεριού του Αρχιμήδη [online]. Ανακτήθηκε στις 10 Ιουνίου 2017 στο cs.drexel.edu.
8. VITE, L. (2014). Αρχή του Αρχιμήδη [online]. Ανακτήθηκε στις 10 Ιουνίου 2017 στο repository.uaeh.edu.mx.