Χαρακτηριστικά τριχοειδών και παράδειγμα στο νερό

Το τριχοθυμία Είναι μια ιδιότητα υγρών που τους επιτρέπει να κινούνται μέσα από σωληνωτές οπές ή πορώδεις επιφάνειες ακόμη και ενάντια στη δύναμη της βαρύτητας. Γι 'αυτό πρέπει να υπάρξει ισορροπία και συντονισμός δύο δυνάμεων που σχετίζονται με τα μόρια υγρού: συνοχή και προσκόλληση. έχοντας αυτά τα δύο μια φυσική αντανάκλαση που ονομάζεται επιφανειακή τάση.

Το υγρό πρέπει να είναι σε θέση να βρέξει τα εσωτερικά τοιχώματα του σωλήνα ή τους πόρους του υλικού μέσω του οποίου κινείται. Αυτό συμβαίνει όταν η δύναμη προσκόλλησης (υγρό τοίχωμα του τριχοειδούς σωλήνα) είναι μεγαλύτερη από τη δύναμη της διαμοριακής συσχέτισης. Κατά συνέπεια, τα υγρά μόρια δημιουργούν ισχυρότερες αλληλεπιδράσεις με τα άτομα του υλικού (γυαλί, χαρτί, κ.λπ.) από ότι μεταξύ τους.

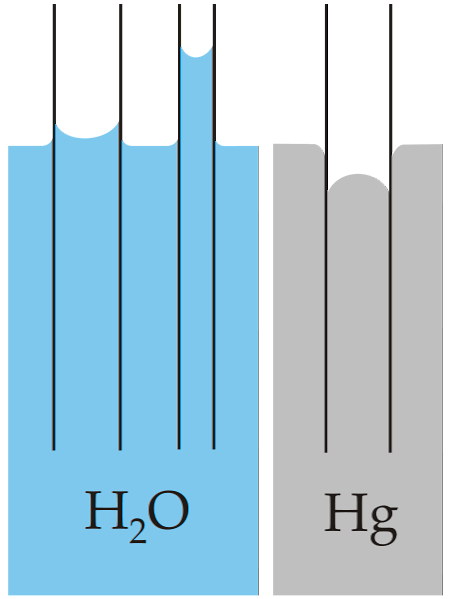
Το κλασικό παράδειγμα της τριχοειδούς παρουσιάζεται στη σύγκριση αυτής της ιδιότητας για δύο πολύ διαφορετικά υγρά: νερό και υδράργυρο.

Η άνω εικόνα δείχνει ότι το νερό ανεβαίνει στα τοιχώματα του σωλήνα, πράγμα που σημαίνει ότι έχει υψηλότερες δυνάμεις πρόσφυσης. ενώ το αντίθετο συμβαίνει με τον υδράργυρο, επειδή οι συνεκτικές, μεταλλικές δυνάμεις συγκόλλησης του εμποδίζουν να βρέξει το γυαλί.

Για το λόγο αυτό το νερό σχηματίζει έναν κοίλο μηνίσκο, και ο υδράργυρος ένας κυρτός μηνίσκος (σχήμα θόλου). Θα πρέπει επίσης να σημειωθεί ότι όσο μικρότερη είναι η ακτίνα του σωλήνα ή του τμήματος μέσω του οποίου κινείται το υγρό, τόσο μεγαλύτερο είναι το ύψος ή η απόσταση που διανύθηκε (συγκρίνετε τα ύψη των κολώνες νερού και για τους δύο σωλήνες).

Ευρετήριο

• 1 Χαρακτηριστικά της τριχοειδούς
  • 1.1 - Επιφάνεια του υγρού
  • 1.2 - Υψος
  • 1.3 -Η τάση της επιφάνειας
  • 1,4-ραδιόφωνο του τριχοειδούς ή πόρου όπου το υγρό αυξάνεται
  • 1.5 - Γωνία επαφής (θ)
• 2 Καταρροϊκότητα του νερού
  • 2.1 Στα φυτά
• 3 Αναφορές

Χαρακτηριστικά της τριχοειδούς

-Επιφάνεια του υγρού

Η επιφάνεια του υγρού, για παράδειγμα το νερό, σε ένα τριχοειδές είναι κοίλη. δηλαδή, ο μηνίσκος είναι κοίλος. Αυτή η κατάσταση συμβαίνει επειδή το αποτέλεσμα των δυνάμεων που ασκούνται στα μόρια του νερού κοντά στο τοίχωμα του σωλήνα κατευθύνεται προς αυτό.

Σε όλους τους μηνίσκους υπάρχει γωνία επαφής (θ), η οποία είναι η γωνία που σχηματίζει το τοίχωμα του τριχοειδούς σωλήνα με μια γραμμή εφαπτόμενη στην επιφάνεια του υγρού στο σημείο επαφής.

Οι δυνάμεις προσχώρησης και συνοχής

Εάν η δύναμη πρόσφυσης του υγρού στο τριχοειδές τοίχωμα επικρατεί πάνω από τη διαμοριακή δύναμη συνοχής, τότε η γωνία είναι θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.

Όταν μια σταγόνα νερού τοποθετείται στην επιφάνεια ενός καθαρού γυαλιού, το ύδωρ επεκτείνεται πάνω στο γυαλί, έτσι ώστε θ = 0 και cos θ = 1.

Εάν η ενδομοριακές δυνάμεις συνοχής υπερισχύει της υγρής-τριχοειδούς τοιχώματος δύναμη προσκόλλησης, για παράδειγμα τον υδράργυρο, ο μηνίσκος είναι κυρτή και η γωνία θ θα έχει μια τιμή> 90? υδραργύρου δεν διαβρέχει το τριχοειδές τοίχωμα και συνεπώς εσωτερικό τοίχωμα του πέφτει.

Όταν μια σταγόνα υδραργύρου τοποθετείται στην επιφάνεια ενός καθαρού γυαλιού, η πτώση διατηρεί το σχήμα της και η γωνία θ = 140 °.

-Ύψος

Το νερό ανεβαίνει μέσω του τριχοειδούς σωλήνα για να φτάσει σε ύψος (h), στο οποίο το βάρος της στήλης ύδατος αντισταθμίζει την κατακόρυφη συνιστώσα της διαμοριακής δύναμης συνοχής.

Καθώς αυξάνεται περισσότερο νερό θα έρθει σε ένα σημείο όπου η βαρύτητα θα σταματήσει την ανοδική της πορεία, ακόμη και με την επιφανειακή τάση που ενεργεί προς όφελος της.

Όταν συμβαίνει αυτό, τα μόρια δεν μπορούν να συνεχίσουν να "ανεβαίνουν" επάνω στα εσωτερικά τοιχώματα και όλες οι φυσικές δυνάμεις εξισώνονται. Από τη μία πλευρά έχετε τις δυνάμεις που προωθούν την άνοδο του νερού, και από την άλλη πλευρά το δικό σας βάρος το πιέζει προς τα κάτω.

Ο νόμος του Jurin

Αυτό μπορεί να γραφεί μαθηματικά ως εξής:

2 π rΥcos = ρgπr²h

Όπου η αριστερή πλευρά της εξίσωσης εξαρτάται από την επιφανειακή τάση, το μέγεθος της οποίας σχετίζεται επίσης με τις δυνάμεις συνοχής ή τις διαμοριακές δυνάμεις. Cos αντιπροσωπεύει τη γωνία επαφής, και r είναι η ακτίνα της οπής μέσω της οποίας το υγρό ανεβαίνει.

Και στη δεξιά πλευρά της εξίσωσης έχουμε το ύψος h, τη δύναμη της βαρύτητας g, και την πυκνότητα του υγρού. αυτό θα ήταν το νερό.

Εκκαθάριση τότε h έχετε

h = (2Ycos / ρgr)

Η διατύπωση αυτή είναι γνωστή ως Jurin Πράξη, η οποία καθορίζει το ύψος που επιτεύχθηκε από τη στήλη υγρού στον τριχοειδή σωλήνα όταν το βάρος της υγρής στήλης με δύναμη αύξουσα εξισορροπείται από τριχοειδούς.

-Επιφανειακή τάση

Το νερό είναι ένα διπολικό μόριο, λόγω της ηλεκτροαρνητικότητας του ατόμου οξυγόνου και της μοριακής του γεωμετρίας. Αυτό προκαλεί το μέρος του μορίου νερού όπου βρίσκεται το οξυγόνο να είναι αρνητικά φορτισμένο, ενώ το τμήμα του μορίου νερού, που περιέχει τα 2 άτομα υδρογόνου, είναι θετικά φορτισμένο.

Τα μόρια εντός του υγρού αλληλεπιδρούν μέσω αυτό με πολλαπλούς δεσμούς υδρογόνου, κρατώντας τα μαζί. Ωστόσο, τα μόρια του νερού που βρίσκονται στο νερό: Τα αέρα (επιφάνεια) υποβάλλεται σε μία καθαρή έλξη των μορίων εντός του υγρού, δεν αντισταθμίζεται από την ασθενή έλξη με τα μόρια του αέρα.

Επομένως, τα μόρια νερού της διεπαφής υποβάλλονται σε μια ελκυστική δύναμη που τείνει να απομακρύνει μόρια νερού από τη διεπαφή. δηλαδή, οι γέφυρες υδρογόνου που σχηματίζονται με τα μόρια στο κάτω μέρος σύρετε αυτά που βρίσκονται στην επιφάνεια. Έτσι, η επιφανειακή τάση επιδιώκει να μειώσει την επιφάνεια της διασύνδεσης νερού: αέρος.

Σχέση με h

Αν κοιτάξετε την εξίσωση του νόμου του Jurin, θα διαπιστώσετε ότι το h είναι άμεσα αναλογικό προς το Υ. Επομένως, όσο μεγαλύτερη είναι η επιφανειακή τάση του υγρού, τόσο μεγαλύτερο είναι το ύψος που μπορεί να ανέλθει μέσω τριχοειδούς ή πόρου υλικού.

Έτσι, μπορεί να αναμένεται ότι για δύο υγρά, Α και Β, με διαφορετικές επιφανειακές τάσεις, το ένα με την υψηλότερη επιφανειακή τάση ανεβαίνει σε υψηλότερο ύψος.

Μπορούμε να συμπεράνουμε από αυτό το σημείο ότι η υψηλή επιφανειακή τάση είναι το πιο σημαντικό χαρακτηριστικό που ορίζει την τριχοειδή ιδιότητα ενός υγρού.

-Ακτίνα του τριχοειδούς ή πόρου όπου το υγρό αυξάνεται

Η παρατήρηση του νόμου του Jurin δείχνει ότι το ύψος που επιτυγχάνεται από ένα υγρό σε ένα τριχοειδές ή πόρο είναι αντιστρόφως ανάλογο με την ακτίνα του ίδιου.

Επομένως, όσο μικρότερη είναι η ακτίνα, τόσο μεγαλύτερο είναι το ύψος που θα φτάσει η στήλη υγρού με τριχοειδή δράση. Αυτό μπορεί να φανεί απευθείας στην εικόνα όπου το νερό συγκρίνεται με τον υδράργυρο.

Σε γυάλινο σωλήνα με ακτίνα ακτίνας 0,05 mm, η στήλη ύδατος με τριχοειδή δύναμη θα φτάσει σε ύψος 30 cm. Σε τριχοειδείς σωλήνες με ακτίνα 1 μm με πίεση αναρρόφησης 1,5 x 10³ Το hPa (το οποίο ισούται με 1,5 atm) αντιστοιχεί σε έναν υπολογισμό του ύψους της στήλης ύδατος από 14 έως 15 m.

Αυτό είναι πολύ παρόμοιο με αυτό που συμβαίνει με εκείνα τα καλαμάκια που περιστρέφονται από μόνο του πολλές φορές. Με το πιπίλισμα του υγρού, δημιουργείται μια διαφορά πίεσης που προκαλεί την άνοδο του υγρού στο στόμα.

Η μέγιστη τιμή ύψους της στήλης που επιτυγχάνεται με τριχοειδή είναι θεωρητική, αφού η ακτίνα των τριχοειδών δεν μπορεί να μειωθεί πέρα ​​από ένα ορισμένο όριο.

Νόμος του Poiseuille

Αυτό αποδεικνύει ότι η ροή ενός πραγματικού υγρού δίνεται από την ακόλουθη έκφραση:

Q = (πρ⁴/ 8η1) ΔΡ

Όπου Q είναι η ροή υγρού, η είναι το ιξώδες του, l το μήκος του σωλήνα και η ΔP η διαφορά πίεσης.

Όταν μειώνεται η ακτίνα ενός τριχοειδούς, το ύψος της στήλης του υγρού που επιτυγχάνεται με την τριχοειδή δύναμη πρέπει να αυξάνεται απεριόριστα. Ωστόσο, ο Poiseuille επισημαίνει ότι η μείωση της ακτίνας μειώνει επίσης τη ροή του υγρού μέσω αυτού του τριχοειδούς.

Επιπλέον, το ιξώδες, το οποίο είναι ένα μέτρο της αντίστασης που αντιτίθεται στη ροή ενός πραγματικού υγρού, θα μειώσει περαιτέρω τη ροή του υγρού.

-Γωνία επαφής (θ)

Όσο μεγαλύτερη είναι η τιμή του cosθ, τόσο υψηλότερο είναι το ύψος της στήλης ύδατος με τριχοειδή ικανότητα, όπως υποδεικνύεται από το νόμο του Jurin.

Αν θ είναι μικρό και πλησιάζει το μηδέν (0), οι cos = 1, έτσι ώστε η τιμή h είναι μέγιστη. Αντιστρόφως, αν θ ισούται με 90 °, τα cos = 0 και την τιμή του h = 0.

Όταν η τιμή του θ είναι μεγαλύτερη από 90, η οποία είναι η περίπτωση του κυρτού μηνίσκου, το υγρό δεν αυξάνεται λόγω της τριχοειδούς και η τάση είναι να πάει προς τα κάτω (όπως ο υδράργυρος).

Καπύλλιο νερού

Το νερό έχει τιμή επιφανειακής τάσης 72,75 N / m, σχετικά υψηλή σε σύγκριση με τις τιμές επιφανειακής τάσης των ακόλουθων υγρών:

-Ακετόνη: 22,75 Ν / μ

-Αιθυλική αλκοόλη: 22,75 N / m

-Εξάνιο: 18,43 Ν / μ

-Μεθανόλη: 22,61 Ν / μ.

Ως εκ τούτου, το νερό έχει μια εξαιρετική επιφανειακή τάση, η οποία ευνοεί την ανάπτυξη του τριχοειδούς φαινομένου τόσο απαραίτητο για την απορρόφηση νερού και θρεπτικών συστατικών από τα φυτά.

Στα φυτά

Η τριχοειδής ικανότητα είναι ένας σημαντικός μηχανισμός για την άνοδο του χυμού από το ξύλο των φυτών, αλλά από μόνη της είναι ανεπαρκής για να φτάσει το χαλίκι στα φύλλα των δέντρων.

Η διαπνοή ή η εξάτμιση είναι ένας σημαντικός μηχανισμός στην ανύψωση του χυμού με το ξύλο των φυτών. Τα φύλλα χάνουν νερό με εξάτμιση, προκαλώντας μείωση της ποσότητας μορίων νερού, γεγονός που προκαλεί την έλξη των μορίων ύδατος που υπάρχουν στους τριχοειδείς σωλήνες (xylem).

Τα μόρια του νερού δεν ενεργούν ανεξάρτητα μεταξύ τους, αλλά που αλληλεπιδρούν με δυνάμεις Van der Waals, πράγμα που καθιστά το εν λόγω ποσό συνδέονται μεταξύ τους με τα τριχοειδή αγγεία των φυτών στα φύλλα.

Εκτός από τους μηχανισμούς αυτούς, θα πρέπει να σημειωθεί ότι τα φυτά απορροφούν νερό από το έδαφος με ώσμωση και θετική πίεση που δημιουργείται από τη ρίζα, προωθεί την αρχή της ανόδου του νερού μέσω τριχοειδών σωλήνων φυτό.

Αναφορές

1. García Franco Α. (2010). Επιφανειακά φαινόμενα. Ανακτήθηκε από: sc.ehu.es
2. Επιφανειακά φαινόμενα: επιφανειακή τάση και τριχοειδής. [PDF] Ανακτήθηκε από: ugr.es
3. Wikipedia. (2018). Καταρροϊκότητα Ανακτήθηκε από: en.wikipedia.org
4. Risvhan T. (s.f.) Capillarity στα φυτά. Ανακτήθηκε από:
5. Helmenstine, Anne Marie, Ph.D. (22 Δεκεμβρίου 2018). Τριχοειδής Δράση: Ορισμός και Παραδείγματα. Ανακτήθηκε από: thoughtco.com
6. Ellen Ellis Μ. (2018). Τριχοειδής Δράση του Νερού: Ορισμός & Παραδείγματα. Μελέτη. Ανακτήθηκε από: study.com
7. Το προσωπικό του ScienceStruck. (16 Ιουλίου 2017). Παραδείγματα που εξηγούν την έννοια και την έννοια της τριχοειδούς δράσης. Ανακτήθηκε από: sciencestruck.com